Trocha lukostřelecké fyziky
Třebaže se fyzice a matematice nebráním, začala mě tahle oblast zajímat ve chvíli, kdy mi začalo vrtat hlavou proč je vlastně reflexní luk lepší než dlouhý, a jestli vůbec je. Takže jak luk funguje?
Síla a hmotnost
Když se u luku mluví o síle, udává se obvykle v librách, nebo občas kilogramech. To jsou ale jednotky hmotnosti, nikoli síly, takže co to znamená? Pokud řekneme, že luk má pri daném natažení sílu 20lb, znamená to, že vyvíjí stejnou sílu, jakou bychom potřebovali pro udržení 20lb závaží nad zemí. Z fyziky všichni víme, že F = m.a, kde a je zrychlení, jaké síla F uděluje tělesu o hmotnosti m. V případě výpočtu síly luku luku se za a dosadí gravitační zrychlení (známých 9,81), a pro výpočet síly nám tudíž stačí znát pouze hmotnost m.
Závislost síly a nátahu
Luk je pružina. Pružina se chová tak, jak říká selský rozum - čím víc ji natáhneme (případně ohneme atd.), tím víc se snaží vrátit zpátky. Tohle nás ale bude u luku zajímat detailněji, a vztah mezi mírou ohnutí ramen (což taky odpovídá míře natažení tětivy) a silou, kterou luk tlačí, budeme zakreslovat do takovéhoto grafu:
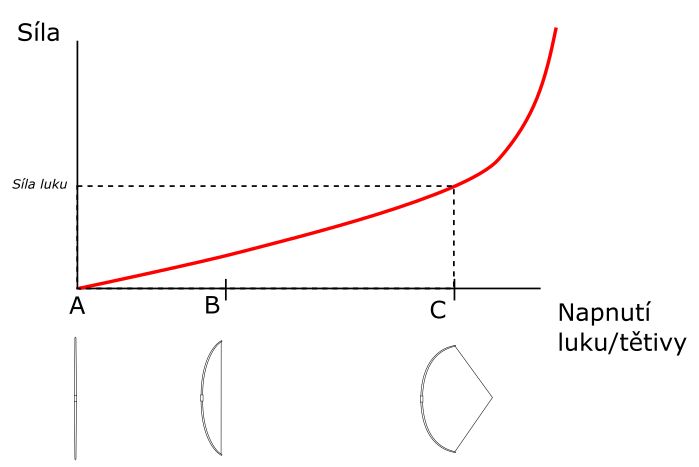
Na ose X je míra ohnutí ramen od výchozího uvolněného stavu, což se lépe představuje jako míra natažení tětivy. Na ose Y je potom síla, jakou se luk při takovém napnutí snaží vrátit. Na osách záměrně nejsou žádná čísla. Nejde nám o to popsat konkrétní luk s konkrétními hodnotami, nýbrž zachytit obecné vlastnosti
Na grafu jsou na ose X tři významné body. Bod A značí luk zcela uvolněný. tato poloha je dána výrobou, a právě do ní se luk po každém napnutí snaží vrátit. Bod B je luk s nasazenou, ale nenapnutou tětivou. Luk tětivu napíná, protože by se rád vrátil do bodu A, ale tětiva mu brání. No a bod C je napětí luku s tětivou napnutou do konstrukcí daného maximálního nátahu. Co je za ním už nás při střelbě nezajímá, protože tam nenatahujem.
Graf ukazuje jakou silou bude luk při dané míře natažení působit. Když luk napínáme od B do C, musíme v každém bodě překonávat sílu, jakou ukazuje graf. To, co se vždy udává jako síla luku, je síla v bodě C. Ale pozor, celý graf funguje i obráceně. Když v bodě C pustíme tětivu, luk se začne prudce vracet k bodu A, a v každém okamžiku tlačí na šíp (prostřednictvím tětivy) silou jakou udává graf. V bodě B se luk zastaví, protože tětiva ho dál nepustí.
Práce
Důležitý ukazatel je jakou vykonáme práci při změně natažení tětivy - typicky při nátahu z bodu B do bodu C. Práce se spočítá při konstantní síle jako F.s (síla . dráha), při nekonstantní (což je náš případ) jako obsah plochy pod grafem závislosti obou veličin. Tato plocha je na obrázku zvýrazněná modře.
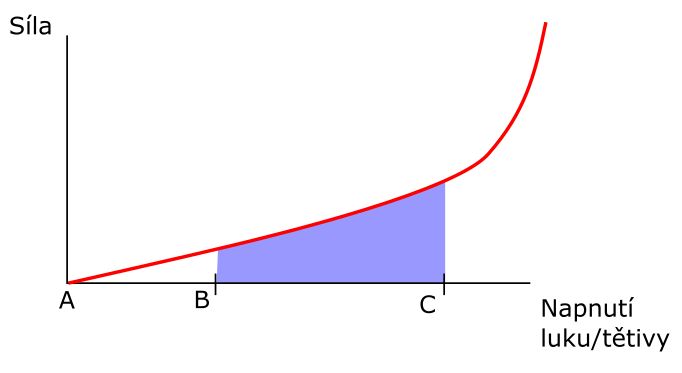
Plocha pod grafem tedy udává práci. Jakou práci? No, čím větší obsah bude plocha pod grafem mít, tím víc si máknem při napínání luku. ALE - když tětivu pustíme, luk tuto práci použije na urychlení šípu. Takže čím víc práce do luku vložíme napínáním tětivy, tím víc ji pak má luk k dispozici k urychlení šípu. A tím je střela účinější a let rychlejší. Účinnější luk se od méně účinného liší tím, že plocha pod grafem je větší, a luk tím pádem vynaloží víc práce na urychlení šípu. Zdůrazňuji,že důležitá je ta plocha pod grafem, NIKOLI síla vyvíjená v bodě C. Ony spolu tyhle dvě hodnoty hodně korespondují, ale ne tak docela, jak vysvětlím u povídání o stackingu a reflexním luku.
Za zmínku stojí další důsledky výpočtu práce. Při pouze částečném nátahu tětivy se nevyužije celá plocha pod grafem mezi body B a C, nýbrž pouze její část.
K urychlení šípu bohužel nevyužije všechna práce - jak už to v reálném světě chodí, všude jsou ztráty. Důležité ztráty práce u luku má na svědomí nutnost táhnout nejen šíp, ale i celou tětivu a ramena luku. Právě ramena luku jsou ten největší žrout - čím jsou těžší, tím víc práce se na jejich uvedení do pohybu spotřebuje, a tím méně jí zbyde na urychlování šípu. Luky, které mají lehká ramena (speciálně na koncích), předají víc síly šípu a tím jsou efektivnější - i když to nelze říct úplně jednoznačně, protože na výsledku se podepisuje i spousta dalších konstrukčních detailů.
Síla luku
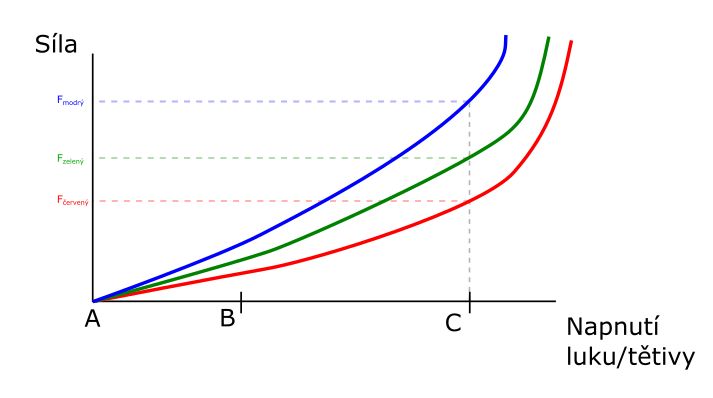
Když se řekne, že luk má sílu 30lb, znamená to, že takovou sílu má při svém maximálním konstrukcí daném nátahu. Graf závislosti pro silnější luk bude strmější, ale pořád bude začínat v nule. Obrázek ukazuje grafy různě silných luků.
Stacking
Představme si dlouhý luk a postup jeho napínání. Když je luk ohnutý příliš, další tah tětivy se snaží ramena spíš natahovat než ohýbat. Tam narazíme na hranici pružících možností, a síla luku v tu chvíli začne prudce růst. U špatně konstruovaných luků (což obvykle znamená příliš krátké přímé luky) nastává stacking už před bodem C. Proč je to špatně? Graf níže ukazuje dva různé luky se stejnou nátahovou silou (oba grafy mají v bodě C stejnou hodnotu). Modrý luk je udělaný dobře, červený špatně (jelikož své síly v maximálním nátahu dosáhl díky stackingu).
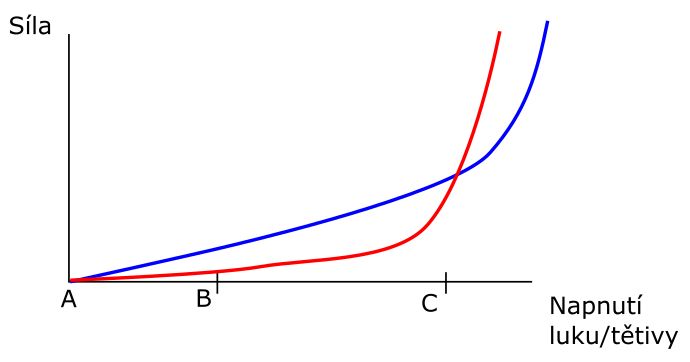
Když porovnáte plochy pod grafem, vidíte že plocha červeného luku je o dost menší. Oba luky bylo v maximálním nátahu stejně těžké udržet, ale červený při výstřelu rychle zeslábnul. Proto by u každého dobře udělaného luku měl stacking nastávat až za bodem C, kde už nás to nezajímá.
Dlouhý a reflexní luk
Teď konečně lze ukázat v čem se reflexní a dlouhý luk liší. Dole jsou grafy pro oba typy luků se stejnou nátahovou silou i se stejnou délkou nátahu.
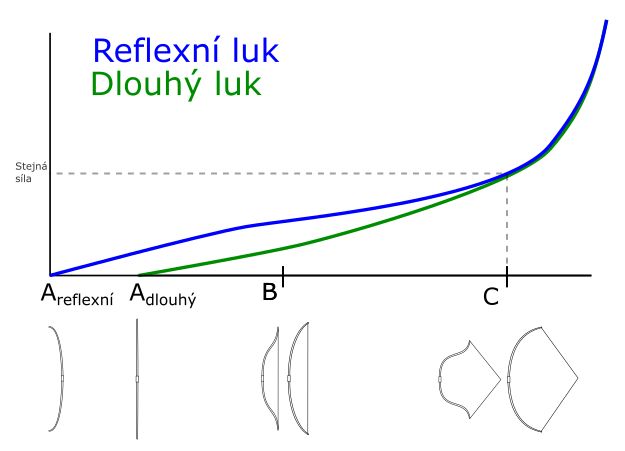
Reflexní luk má v uvolněném stavu konce ramen víc předsunuté (bod A je od bodů B a C dál),což posouvá celý graf doleva. Teoreticky by to mělo doleva posouvat i oblast stackingu, tím spíš, když uvážíme, že reflexní luky bývají o kus kratší. Jenže to se nestane. Proč? No, může za to to esovité prohnutí ramen. Stacking nastává v okamžiku, kdy se luk tahem ve směru tětivy už dál nedá dobře ohnout. U reflexního luku ale zahnutý konec ramene funguje jako páka, která při velkém napnutí pomáhá rameno dále ohýbat. Celé esovité rameno je také schopné se natahovat, tudíž pruží ještě v dalším směru. Celé to dohromady účinně odsouvá stacking dál, až za hranici maximálního nátahu.
Celý graf je tím pádem celý protaženější a méně strmý - už v bodě B je síla docela velká, a cestou do C se mění už jen trochu. I když je síla v bodě C stejná jako u dlouhého luku, při výstřelu bude pomaleji klesat. Reflexní luk tak při stejné nátahové síle dokáže vykonat při urychlování šípu větší práci, a proto je výkonější. Ovšem tahle výhoda není zadarmo - aby to fungovalo, ramena musí pružit mnohem líp, než zvládne jakékoli dřevo.

